题目: \(\text { 试证明 } \lim _{n \rightarrow+\infty} \int_{0}^{\frac{\pi}{2}} \sin ^{n} x \mathrm{~d} x=0 \text {. }\)
解答:
首先从图像中观察
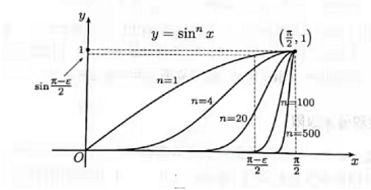
从图中可以看出, 由于 $\sin \frac{\pi}{2}=1$, 因此对每个 $n$, 当 $x$ 与 $\frac{\pi}{2}$ 充分接近时, 函数 值 $\sin ^{n} x$ 一定接近 1 . 另一方面, 对于固定的 $x$ 值, 只要 $x$ 小于 $\frac{\pi}{2}$, 则当 $n$ 增加时 函数值 $\sin ^{n} x$ 就很快趋于 0 . 这就是下面的 “分而治之”方法的几何背景.
\[\begin{aligned} 0 & \leqslant \int_{0}^{\pi / 2} \sin ^{n} x \mathrm{~d} x=\int_{0}^{(\pi-\varepsilon) / 2} \sin ^{n} x \mathrm{~d} x+\int_{(\pi-\varepsilon) / 2}^{\pi / 2} \sin ^{n} x \mathrm{~d} x \\ & \leqslant \frac{\pi}{2} \sin ^{n} \frac{\pi-\varepsilon}{2}+\frac{\varepsilon}{2} . \end{aligned}\]由 \(0<\sin \frac{\pi-\varepsilon}{2}<1, 可见 \lim _{n \rightarrow \infty} \sin ^{n} \frac{\pi-\varepsilon}{2}=0\)
\[从面对上述 \varepsilon, \exists N, 使n>N 时, 成立 0<\frac{\pi}{2} \sin ^{n} \frac{\pi-\varepsilon}{2}<\frac{\varepsilon}{2}.\]因此 $ n>N $ 时, 就有 \(0 \leqslant \int_{0}^{\pi / 2} \sin ^{n} x \mathrm{~d} x<\varepsilon\)
==注 1==
利用上、下极限工具, 还可将证明写得简洁一些. 不等式中直接令 $n \rightarrow \infty$, 就得到
利用 $\varepsilon>0$ 的任意性, 可见上、下极限相等且为 0 .
==注 2==
在分拆积分时可以平取动态方法, 按照区间
\(\left[0, \frac{\pi}{2}-\frac{1}{\sqrt[3]{n}}\right] \text { 和 }\left[\frac{\pi}{2}-\frac{1}{\sqrt[3]{n}}, \frac{\pi}{2}\right]\)
拆成两个积分, 然后分别证明它们 (作为数列) 当 $n \rightarrow \infty$ 时的极限是 0 . 读者可以一试,
==注 3==
本题的常见错误如下: 证 由积分第一中值定理, $\exists \xi \in\left(0, \frac{\pi}{2}\right)$, 使得
\[\int_{0}^{\pi / 2} \sin ^{n} x \mathrm{~d} x=\sin ^{n} \xi \int_{0}^{\pi / 2} \mathrm{~d} x=\frac{\pi}{2} \sin ^{n} \xi .\]不难看出一定有 $0<\sin \xi<1$ 成立, 因此得到
\[\lim _{n \rightarrow \infty} \int_{0}^{\pi / 2} \sin ^{n} x \mathrm{~d} x=\lim _{n \rightarrow \infty} \frac{\pi}{2} \sin ^{n} \xi=0 .\]==错误分析==
错误在于 $\xi$ 不是常数, 而是随着 $n$ 的变化而变化的, 应该记为 $\xi_{n}$. 当 $n \rightarrow \infty$ 时, 不难证明有 $\xi_{n} \rightarrow \frac{\pi}{2}$, 因此 $\sin ^{n} \xi_{n}$ 是 $1^{\infty}$ 型的不定式. 回忆数列极限的内容, 我们知道, 从一个数列 \(\left\{a_{n}\right\}\)
的每一项满足 $0<a_{n}<1$ 是得不出 \(\lim _{n \rightarrow \infty} a_{n}^{n}=0\) 的 (试举例).